
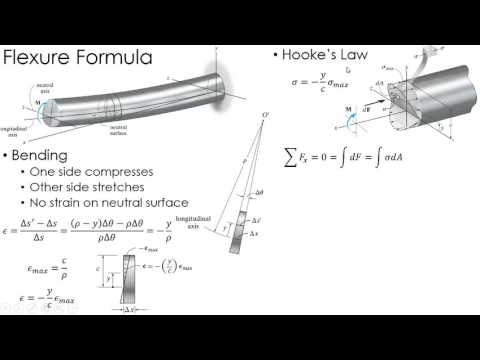
Putting all three terms together, equation 1 becomes: P Le t 2 = 6 P Le 3 bt bt 2 12Įquation 3 Equation 3 is only valid for the surface of an end-loaded cantilever beam with a rectangular cross-section. M refers to the bending moment and in an elementary uniaxial setup is equal to the applied force P multiplied by the effective length, Le. c is replaced by half of the beam's thickness. I is dependant on the beam geometry, and in this case is equal to:Įquation 2 where b is the width and t is the thickness. Since all three terms are calculated, it is easier to replace each term with terms representing terms physically measured. To do so, the flexure formula can be used.Įquation 1 Where M is the bending moment at the point of interest (measured in inch-pounds or Newton-meters), c is the distance from the neutral axis to the surface (measured in inches or meters), and I is the centroidal moment of inertia measured around the horizontal axis (inches4 or meters4). With a known force, beam, and strain, and resulting stress can be calculated. A strain gage should be located perpendicular, as well as a known distance, from the applied force. This is achieved by supporting a beam in a cantilever setup while applying pressure to a point on the beam. A simple way of determining the Young's modulus is to create a uniaxial stress state. For the purposes of testing the Young's modulus, the applied load should be kept below the yield strength, the pressure as which a material begins to experience plastic deformation. The phenomena occurring during this sudden change in slope is known as plastic deformation and is beyond the scope of this lab. With excessive loading, the stress-strain curve initially begins linearly, followed by a dramatic change of slope. Experimentally, the modulus of elasticity, or Young's modulus, is found by determining the slop of the stress versus strain curve. This can also be thought of as the amount of deformation a material undergoes when subjected to a load. Introduction & BackgroundThe modulus of elasticity refers to a material's stiffness.
MECHANICS OF MATERIALS FLEXTURE EXAMPLES HOW TO
The following experiment demonstrates how to ascertain the modulus of elasticity for a material by determining this characteristic for 2024-T6 aluminum.
This number, in units of pressure, can be used to predict such behaviors as deflection, stretching, and buckling. The stiffness can be characterized by a parameter known as the modulus of elasticity, or Young's modulus. Mechanics of Materials Laboratory Lab #4 Modulus of Elasticity Flexure TestĪbstractSince all materials experience some type of deformation when external forces act upon them, it is important to understand the behavior and limitations of these materials.


 0 kommentar(er)
0 kommentar(er)
